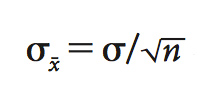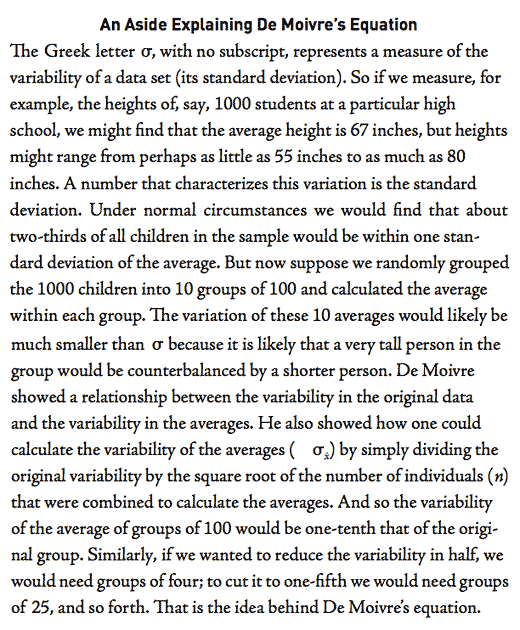They grab wafers between which are wedged lumps of coal and copper snow. Sucking, they scatter slowly.

What constitutes a dangerous equation? […] Few would disagree that the obvious winner in this contest would be Einstein’s iconic equation
E=MC2
for it provides a measure of the enormous energy hidden within ordi- nary matter. Its destructive capability was recognized by Leo Szilard, who then instigated the sequence of events that culminated in the construction of atomic bombs.
This is not, however, the direction I wish to pursue. Instead, I am interested in equations that unleash their danger, not when we know about them, but rather when we do not; equations that allow us to understand things clearly, but whose absence leaves us dangerously ignorant.* There are many plausible candidates that seem to fill the bill. But I feel that there is one that surpasses all others in the havoc wrought by ignorance of it over many centuries. It is the equation that provides us with the standard deviation of the sampling distribution of the mean; what might be called De Moivre’s equation:
For those unfamiliar with De Moivre’s equation let me offer a brief aside to explain it.
Why have I decided to choose this simple equation as the most dangerous? There are three reasons, related to
(1) the extreme length of time during which ignorance of it has caused confusion,
(2) the wide breadth of areas that have been misled, and
(3) the seriousness of the consequences that such ignorance has
caused.
photo { Adam Broomberg & Oliver Chanarin }